小数老师说 也会是小数老师研究北京的题目太多了,近期几年没看到这种问题,不过既然在微信平台上有同学提问了,那小数老师就帮这个同学整理一下吧!小数老师研究了一下,全国卷考这种题目还是比较多的,但目前的困难程度也比小数老师上学时的简单了不少了! 找了近期的一些题目看了看,棱锥的外接球问题一般分为两类:已知棱锥的有关条件,求外接球的表面积或者体积等;已知棱锥的外接球的一些条件,求棱锥的有关信息!下面通过两道例题来看一下,这种题目该怎么样求解! 1、已知棱锥,求外接圆 例1、已知三棱锥P-ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,PC为球O的直径,该三棱锥的体积是 ,则球O的表面积是() A、4B、8C、12D、16 分析:本题已知三棱锥的体积与底面边长,求球O的表面积,其实说白了,就是需要找到外接球的半径,再借助公式就能得出结果了。所以,第一步就是画图,
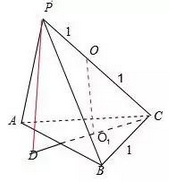
通过题目大家可以了解,此三棱锥的底面为等边三角形,那样就能了解,假如过点P向底面做垂线的话,垂足肯定落在三角形ABC的边BC的高上,也就是图中的CD上,因为PC是外接球的直径,因此取中点O,然后找到三角形ABC的外接圆的圆心C,O也在CD上,所以能得到OO垂直于CD,所以OO与PD平行,且OO等于PD的一半,PD是三棱锥的高,依据三棱锥的体积就能求出高来,因此OO的值也能求出来,而三角形OOC是直角三角形,OC是三角形ABC高的三分之二,因此列出方程,球的半径就能求了。 具体解题步骤同学们自己补全吧! 答案选择:A 例2、已知正四面体ABCD的棱长为a,其外接球表面积为S1,内切球表面积为S2,则S1:S2的值为() A、3B、 C、9D、 分析:正四面体为载体,同学们真是沾大光了哈,棱长与底边都相等,其性质也特别好,外接球的球心与内切球的球心是一个,都在正四面体的高上,下面画图找几何性质即可。
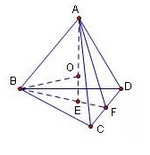
如图:点O是正四面体外接球与内切球的球心,并且BO为外接球的半径,OE为内切球的半径,三角形BOE为直角三角形,E点为三角形BCD的边CD上的高BF上的点,并且BE:EF=2:1,所以,依据这类条件进行列方程即可求出比值来。 答案选择:C 2、已知外接圆,求棱锥 例3、已知三棱锥P-ABC的四个顶点都在半径为2的球面上,且PA平面ABC,若AB=2,AC= ,BAC= ,则棱PA的长为() A、 B、 C、3 D、9 分析:通过题意,可以得出三棱锥为墙角型的,如图:
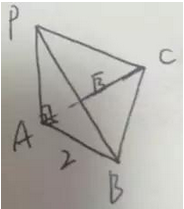
对于墙角型三棱锥,探寻外接球一般采取补形法,也就是以AB,AC,PA为边做出长方体来,长方体的外接球与此三棱锥的外接球相同,而对于长方体来讲,其外接球的直径为长方体的体对角线,体对角线l与长方体的长a宽b高c的关系是: ,通过此关系,列方程即可得到结果。 答案选择:C。 以上就是小数老师给大伙的三个例题,同学们可以发现,无论是哪类型型,重点是要找到球心,也就是要把三棱锥的几何性质搞了解,同学们也不需要担忧,目前试题都不是非常难,大伙重点研究正三棱锥,正四面体,和墙角型的三棱锥就足以应付了!加油吧! 有哪些想看的,欢迎大伙发信息哈,小数老师精力有限,可能总结的不是那样全方位,但小数老师肯定以高考考试题为参考试试题型来剖析每一个要点的哈! 原创不容易,请同学们动动手指,转发到你的朋友圈,让更多的同学看到!另外,如有转载,请标明来自高中数学公众号,谢谢!
推荐阅读:
2016高考考试资讯 | 2016艺考 | 2016自主招生 | 2016中国大学排名推荐 | 最好看的校花整理
1月高考考试关注:特殊种类招生与港澳高校中国大陆招生
中国校友会网:2016年中国各种类大学排名推荐
2016年全国高考考试考试概要权威解析(共9科)
25所高校招办解析2016年艺术类专业招生政策
调查称2015年高校毕业生月起薪平均为4187元
武汉大学女神黄灿灿 清纯扮相引人眼球(组图)


